Introducción

En medicina, con frecuencia se busca comparar dos métodos diferentes de medición, ya sea entre un método nuevo con uno probadamente efectivo, o entre dos que se utilizan para medir lo mismo. Un ejemplo podría ser cuando se comenzó a utilizar la evaluación de presión arterial con esfigmomanómetros digitales, y se comparaban sus resultados con un esfigmomanómetro de mercurio. Las razones del por qué hacer estas comparaciones son muchas: un nuevo método menos invasivo, más barato, rápido, o accesible que el anterior. Lo que se quiere responder es si los dos métodos concuerdan lo suficientemente bien o no en sus mediciones.

En la práctica, los análisis de comparación habían sido frecuentemente basados en análisis con coeficientes de correlación, pero estos métodos fueron consistentemente criticados en la literatura metodológica [1],[2],[3],[4]. En 1983, Altman y Bland plantearon su visión respecto a la comparación de dos métodos, e hicieron énfasis en que el análisis con correlación de Pearson no era el método más adecuado [1]. Se basaban en el hecho que la correlación de Pearson no evalúa concordancia entre las mediciones, sino que evalúa asociación lineal entre las mediciones (variables), por lo que dos métodos pueden correlacionarse muy bien, pero sin embargo concordar muy poco [1]. A continuación se desarrollará esta idea.

Coeficientes de correlación y sus limitaciones

Las razones del por qué el análisis con coeficientes de correlación no es el más adecuado se centran en el hecho que su cálculo depende principalmente de la variabilidad entre sujetos [5], no provee información sobre el tipo de asociación, y es muy sensible al rango de valores en estudio [4], es decir, rangos mayores de valores de las mediciones informarán coeficientes sobreestimados [6]. Además, las pruebas de correlación son medidas de asociación y no de concordancia, por lo que no informan si las diferencias entre las mediciones son sistemáticas o al azar [4],[5]. Por último, valores altos (cercanos a 1) en las pruebas de correlación pueden esconder errores de medida de importancia clínica, y en definitiva no traducen necesariamente buena concordancia [5]. La interpretación inadecuada de una prueba de correlación se manifiesta en que en algunas publicaciones se concluye que existe una adecuada concordancia entre dos mediciones por el valor de p de la prueba de correlación (cuando es significativo), independiente del valor de su coeficiente [7]. Sin embargo, es necesario tener cautela con esto, en la medida que la hipótesis de nulidad de las pruebas de correlación es que no existe tal, por lo que dependiendo del tamaño muestral, cualquier coeficiente diferente de 0 puede ser significativo, lo cual no parece tan difícil en la medida que las dos mediciones se refieren a lo mismo. Es decir, no sólo se evalúan con métodos no adecuados, sino que además se concluye en base al valor de p y no al coeficiente de correlación.

Para ejemplificar esto, para los fines de este artículo se simularon datos de 150 pacientes con sus respectivas presiones arteriales sistólicas. El método de referencia (R) informó un promedio (desviación estándar, DE) de presión arterial sistólica fue 132,5 (+ 8,6) mm/Hg, con una distribución normal (Shapiro Wilk p=0,426). Se compararon estos datos con datos obtenidos mediante 2 esfigmomanómetros digitales E1 y E2, para los mismos pacientes. El primero (E1) mide adecuadamente la presión arterial sistólica, con concordancia en la mayoría de los individuos (promedio 132,4 (+ 8,6) mm/Hg), mientras que el segundo mide consistentemente 5 mm/Hg más elevado que el método de referencia para todos los individuos excepto para el primero (promedio 137,4 (+ 8,6) mm/Hg). Se evaluaron las 3 pruebas de correlación más usadas (tabla 1). Se observa que todos los coeficientes de correlación informaban valores cercanos a 1, lo que desde el punto de vista de la correlación podría ser considerado como una excelente asociación entre la medida y su referencia. Incluso se podría haber planteado que el método E2 concordaría mejor con el método de referencia, a pesar que sabemos que estima 5 mm/Hg más en casi todas las observaciones. En este caso, el error sistemático de E2 no es detectado por las pruebas de correlación [5]. Algo similar hubiese ocurrido si el método E2 hubiese informado valores que se alejaran en la misma medida hacia los extremos desde el valor central. Sin embargo, las mediciones no concuerdan en la medida que las mediciones simultáneas para cada individuo no fueron iguales, por lo que el análisis con correlación puede llevar a obtener una conclusión incorrecta. Por último, como los coeficientes de correlación (en particular el de Pearson) se construyen a partir de pares ordenados de mediciones, si varía el orden varía el valor del coeficiente, pero un cambio en las escalas de medida no afectará este pero si afectará la concordancia [6]. A comienzos de los años 80, Altman y Bland plantearon que la correlación no era un análisis de concordancia, sino de asociación lineal, e hicieron cuestionamientos similares a los análisis con regresión lineal [1]. Con el tiempo, su método se convertiría en el estándar de oro estadístico para evaluar concordancia, e incluso en el sexto artículo más citado de estadística [8].

Tabla 1. Comparación entre dos métodos de medición de presión arterial sistólica contra datos de referencia (n=150) (datos simulados).

Respecto al análisis de datos categorizados, o de escalas tipo Likert, se ha argumentado que la comparación de estos datos se podría hacer con pruebas de correlación, mediante la comparación de los rankings de las distintas categorías. Sin embargo, las pruebas de correlación fallan en evaluar concordancia en este tipo de datos también [5].

Método de Bland-Altman

Altman y Bland plantearon una manera más apropiada para analizar la concordancia, la que posteriormente se denominaría “límites de concordancia” [9]. El fundamento era evaluar si la comparación de los métodos permitía que uno reemplazara al otro con la suficiente precisión. Para esto había que considerar dos aspectos clave: cuan bien los métodos concuerdan en promedio, y cuan bien concuerdan para los individuos [9],[10].

La concordancia promedio se evalúa comparando el promedio de las diferencias de las mediciones de los individuos. Esto se puede realizar con una prueba de t de Student para muestras pareadas o con una prueba de Wilcoxon (en caso de no ser paramétrica), tomando como hipótesis de nulidad la no diferencia. La estimación de la diferencia se puede informar con intervalos de confianza (IC) de 95% (IC95%), la que se obtiene como la [diferencia promedio + 1,96 X el error estándar de las diferencias] [9]. En el ejemplo, la diferencia entre R (132,5 (+ 8,6) mm/Hg) y E1 (132,4 (+ 8,6) mm/Hg) no fue significativa (t de Student pareada p=0,5), y entre R y E2 (137,4 (+ 8,6) mm/Hg) si lo fue (diferencia de promedios de -4,96; p<0,0001). Es decir, no hubo diferencia en el promedio de la mediciones entre el método de referencia y el método que mide adecuadamente (E1), pero sí la hubo entre el de referencia y el que mide consistentemente más alto (E2), lo que era esperable.

Para evaluar la concordancia para individuos es necesario evaluar la variabilidad de las diferencias. En primer lugar, se debe analizar la distribución de las diferencias, lo que se puede hacer mediante un histograma o una prueba de distribución. En caso de seguir una distribución normal, se calculan los límites de concordancia como el [promedio de las diferencias + 1,96 X la desviación estándar de las diferencias] [9]. Si la distribución de las diferencias es relativamente normal, el error sistemático se evalúa con el promedio de las diferencias, y el error al azar con la desviación estándar de las diferencias [5].

Posteriormente, se grafican estos límites de concordancia en un diagrama de puntos de la diferencia entre mediciones (eje y) contra su promedio (eje x) (diagrama de Bland-Altman). Este se debe evaluar observando si existe alguna relación entre la diferencia (eje y) y el nivel de medición (evaluado por el promedio de las mediciones, eje x). Este gráfico cuantifica el rango de valores que puede incluir la concordancia para la mayoría de los sujetos. Lo que se espera encontrar es que los puntos se distribuyan sin seguir un patrón definido, como por ejemplo una relación directa o inversa entre las variables. En caso de observar alguna relación, como podría ser que a medida que aumenta el promedio aumente la diferencia entre los métodos, o que a medida que aumente el promedio aumente la variabilidad de las diferencias, Bland y Altman propusieron posteriormente la utilidad de las técnicas de transformación o de regresión para mejorar eso [11],[12]. La interpretación de los límites de concordancia es que para un individuo seleccionado al azar de la población sobre la que se espera inferir los resultados, se espera que la diferencia entre las dos evaluaciones se encuentre entre los límites con un 95% de probabilidad. Luego, si las diferencias entre los dos métodos, considerando estos límites, no son clínicamente relevantes, el método nuevo podría ser usado en reemplazo del anterior. Con los datos simulados, el gráfico para E1 y E2 contra R se aprecia en las figuras 1 y 2. A pesar que impresiona que la figura 1 tiene más valores fuera de los límites de concordancia, estos representan menos de un 10% de las observaciones, pero la diferencia de los niveles de medición prácticamente no existe (por eso la "diferencia" está en torno a 0, mismo motivo por el que al aplicar la t de Student pareada del párrafo anterior no se encontró una diferencia entre las mediciones). Por el contrario, la figura 2 prácticamente no tiene valores que se escapen demasiado de los límites de concordancia, pero al evaluar la diferencia de los niveles de medición, se aprecia una diferencia de 4,96 unidades (mmHg), la que es significativa (p<0,0001); es decir, se "mueve" más parecido a la medición de referencia, pero siempre en un valor mayor.

Figura 1. Gráfico de Bland-Altman evaluando concordancia entre un método de referencia (R) y un primer método de medición alternativo (E1) para estimar presión arterial, en mmHg.

Figura 2. Gráfico de Bland-Altman evaluando concordancia entre un método de referencia (R) y un segundo método de medición alternativo (E2) para estimar presión arterial, en mmHg.

Además, los límites superior e inferior de los límites de concordancia se pueden informar con sus respectivos intervalos de confianza de 95%, lo que proporciona una mejor cobertura de los valores reales esperados en la población sobre la que se espera inferir. Una simulación con 10 000 repeticiones observó que los límites por sí solos incluían en promedio al 65% de los valores, mientras que con los intervalos de confianza, se elevaba esto a valores más reales (97,5% - 98,6%) [8]. En cualquier caso, es importante recalcar que la importancia de esto es que permite evaluar mejor el rango de valores de concordancia, pero no proporciona un criterio sobre el cual validar los métodos.

Una excepción relevante de mencionar, es que el método de Bland-Altman asume que las varianzas de ambas mediciones sean relativamente similares, y por ende las varianzas de sus errores al azar. En caso de que esto no suceda, dos mediciones pueden concordar bastante bien, y sin embargo el gráfico puede mostrar una tendencia espuria [13]. En estas situaciones, los gráficos se deben interpretar teniendo esto en consideración.

Discusión

A pesar de lo discutido, siguen existiendo algunos errores reportados al evaluar concordancia. Dentro de estos se incluye el considerar que el método de los límites de concordancia es un complemento del uso de la correlaciones tradicionales para la comparación de dos métodos, por lo que informan el valor del coeficiente de correlación (en el caso de una correlación de Pearson, el r) y el diagrama de Bland-Altman [14]. En otros casos, se ha visto que se considera al diagrama en sí mismo como el análisis, sin considerar los supuestos ni la concordancia promedio [9]. Una revisión que evaluó 46 estudios de validación entre el 2000 y el 2005, encontró que en el 89,1% de estas, se seguían usando pruebas de correlación para evaluar concordancia, y que sólo el 21,7% usaba el método de Bland-Altman [5].

Hay que considerar que la diferencia máxima entre los métodos es una decisión clínica, no estadística. Es decir, una diferencia de 5 mm/Hg en la presión arterial sistólica entre dos métodos para medir presión arterial ambulatoria quizás sería aceptable, pero esa misma diferencia para métodos para medir la presión arterial con un catéter intra arterial, no lo sería. Los límites de concordancia informan valores, pero estos no deben ser considerados como un criterio para definir si la diferencia máxima es aceptable o no [15]. La principal utilidad de los límites de concordancia es evaluar si la concordancia entre las mediciones es buena o no, lo que se hace evaluando la dispersión de los puntos, pero no establece hasta qué rango es aceptable. No existe ningún método que permita establecer esto, sólo el juicio clínico y el análisis de los resultados de esta estimación [8].

Es importante que los estudios clínicos para comparar métodos tengan el tamaño muestral necesario. Si el número de individuos es pequeño, incluso grandes diferencias entre los métodos no serán detectadas, por lo que existe la posibilidad de considerar que un nuevo método es adecuado aun cuando no lo sea en verdad. Se recomienda que los estudios de comparación tengan al menos 100 individuos, con una medición de cada método para cada uno [9].

Otra herramienta que con frecuencia se utiliza es el coeficiente de correlación intraclase, el que representa una variación de los coeficientes de correlación tradicionales en la medida que provee una medida compuesta que considera tanto la variabilidad inter como intramétodo para variables cuantitativas [16]. Este estima el promedio de las correlaciones entre todas las posibles ordenaciones de los pares de observaciones disponibles y, por lo tanto, evita el problema de la dependencia del orden del coeficiente de correlación [17]. Sin embargo, se han mencionado limitaciones en su uso, como la dificultad en su cálculo en la medida que esta depende del diseño del estudio, el hecho de ser una prueba paramétrica por lo que se requiere que se cumplan ciertos supuestos, la dependencia de la variabilidad de los valores observados, y sobre todo la dificultad de su interpretación clínica [16],[18]. En cualquier caso, representa una medida diferente al método de Bland-Altman, que podría ser complementaria, pero no necesaria para el cálculo de los límites de concordancia. Además, los coeficientes de correlación, coeficiente de correlación intraclase, regresiones lineales, y el índice kappa, dependen de la varianza o de la prevalencia de la medición en la población de la cual se obtuvo la muestra, mientras que el método de Bland-Altman es independiente de la población seleccionada [5].

Conclusiones

En conclusión, la utilización de pruebas de correlación es un método poco adecuado para evaluar concordancia. Un método más correcto es la utilización de los límites de concordancia, que incluye la concordancia promedio, evaluación de la dispersión de diferencia entre los individuos, y los diagramas de Bland-Altman, lo que grafican la diferencia entre dos mediciones contra su promedio. Además, permite evaluar tanto los errores sistemáticos como los por azar, ya sea en caso de comparación entre dos mediciones, calibraciones, o medidas repetidas [4].

Notas

Declaración de conflictos de intereses
El autor ha completado el formulario de declaración de conflictos intereses del ICMJE traducido al castellano por Medwave, y declara no haber recibido financiamiento para la realización del reporte; no tener relaciones financieras con organizaciones que podrían tener intereses en el artículo publicado, en los últimos tres años; y no tener otras relaciones o actividades que podrían influir sobre el artículo publicado. Los formularios pueden ser solicitados contactando al autor responsable o a la dirección editorial de la Revista.

Financiamiento
El autor declara que no hubo fuentes de financiación externas.

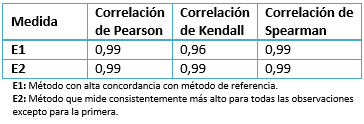Tabla 1. Comparación entre dos métodos de medición de presión arterial sistólica contra datos de referencia (n=150) (datos simulados).

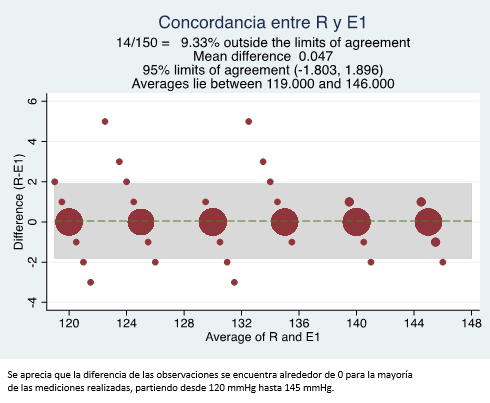Figura 1. Gráfico de Bland-Altman evaluando concordancia entre un método de referencia (R) y un primer método de medición alternativo (E1) para estimar presión arterial, en mmHg.

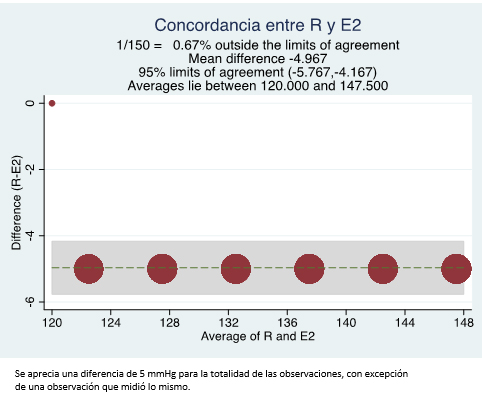Figura 2. Gráfico de Bland-Altman evaluando concordancia entre un método de referencia (R) y un segundo método de medición alternativo (E2) para estimar presión arterial, en mmHg.

Esta obra de Medwave está bajo una licencia Creative Commons Atribución-NoComercial 3.0 Unported. Esta licencia permite el uso, distribución y reproducción del artículo en cualquier medio, siempre y cuando se otorgue el crédito correspondiente al autor del artículo y al medio en que se publica, en este caso, Medwave.