I. Introducción

En determinados estudios epidemiológicos el foco de interés se centra en la determinación de factores de riesgo para una determinada condición de salud. Una pregunta relevante que se desprende de la correspondiente a la determinación de estos factores de riesgo, tiene que ver con el grado de independencia de la asociación demostrada entre el evento de salud de interés y sus factores de riesgo de otras características de los sujetos seleccionados para el estudio.

En este artículo se presenta una estrategia de modelamiento estadístico que permite determinar si uno o más factores de exposición constituyen un factor de riesgo o de protección para una determinada condición de salud y su dependencia de otras características de los sujetos en estudio.

A  modo de ejemplo, supongamos que se desea determinar si el consumo de alcohol y el consumo de tabaco son factores de riesgo para cáncer de esófago. Adicionalmente se desea determinar si el eventual efecto que tenga el consumo de alcohol y de tabaco sobre el cáncer de esófago es independiente de la edad y sexo en una muestra de sujetos de una determinada población.

II. Definición de variables en un modelo de regresión.

Un modelo de regresión no es más que una representación estadístico matemática de una expresión analítica correspondiente a una pregunta de investigación que considera uno o más factores de exposición (candidatos a factor de riesgo o de protección) para un evento de salud -que para simplificar, puede que esté presente o ausente en cada uno de los sujetos en estudio- y un conjunto de otros factores externos a la relación de interés. En el ejemplo más arriba enunciado, tenemos que el evento de salud es cáncer de esófago, los factores de exposición son consumo de alcohol y consumo de tabaco, y la edad y sexo las correspondientes variables de control.

Este problema puede representarse gráficamente como se muestra en la Figura 1 siguiente.

Figura 1. Esquema de variables del estudio de asociación.

De ahora en adelante, se continuará con el ejemplo anterior para desarrollar la idea del modelo estadístico que dé respuesta a la pregunta de investigación.

III. Estrategia de modelamiento

La primera decisión tiene que ver con la elección del modelo estadístico a utilizar,  que depende principalmente del nivel de medición de la variable de respuesta. En este caso particular la variable de respuesta es presencia o ausencia de cáncer de esófago, de tipo dicotómica. En una muestra probabilística de sujetos de una población determinada, el interés se centra entonces en  poder estimar la proporción de sujetos que presenta cáncer de esófago o la odds de presentar dicha enfermedad en sujetos expuestos o no a los factores identificados en la pregunta de investigación como potenciales factores de riesgo/protección de cáncer de esófago.

Dependiendo del diseño de investigación utilizado para la generación de los datos, se podría entonces estimar medidas de asociación que permitan evaluar si los factores de exposición, consumo de alcohol y consumo de tabaco, constituyen un factor de riesgo o de protección para cáncer de esófago, considerando además que los sujetos en estudio tienen diferentes edades y sexos y que estas características pudieran no estar balanceadas entre las categorías tanto de la variable de repuesta como entre las de las variables de control.

Asumamos de aquí en adelante, que la medida de asociación de interés es la razón de odds (odds ratio, OR), definida en este caso como el cociente entre la odds de cáncer de esófago en expuestos y la odds de cáncer de esófago en no expuestos. El modelo estadístico que permite estimar razón de odds es el conocido como modelo de regresión logística múltiple [1],[2],[3].

Para la elaboración del modelo se debe especificar cuál es la variable de respuesta (cáncer de esófago), cuales son los factores de exposición (consumo de alcohol y consumo de tabaco) y cuáles son los otros factores de control (edad y sexo). Dado que en la presentación del problema se establece que el potencial efecto de los factores de exposición sobre el cáncer de esófago pudiera o no depender de edad y sexo, es necesario incluir en el modelo los términos que permitan dar cuenta de esto. Estos términos corresponden a las llamadas interacciones entre los factores de exposición y las variables de control (por simplicidad se asume que no hay interacción entre los factores de exposición). La interacción entre dos variables se construye como el producto entre ellas.

Para comenzar a dar respuesta a la pregunta, se recomienda especificar el rol de cada una de las variables a ser incluidas en el modelo. De esta forma, se procede a identificar la variable de respuesta, las variables de exposición, las variables de control y las variables de interacción. La siguiente tabla muestra la especificación de las variables de ejemplo.

Tabla 1. Especificación de las variables del Modelo.

La inclusión de estas variables de interacción corresponde a la eventualidad de que el efecto de los factores de exposición dependa de cada una de las variables definidas como de control. Por ejemplo, la interacción alcohol*sexo, de ser distinta de cero, indica que el efecto del consumo de alcohol en el cáncer de esófago es distinto en hombres y mujeres, lo que debiera reflejarse en una diferencia entre la razón de odds de cáncer de esófago entre los que consumieron alcohol y los que no consumieron alcohol no es la misma en hombres que en mujeres.

Definidas las variables de esta forma, se procede ahora a la especificación analítica del modelo, que en este caso corresponde a uno logístico múltiple cuya expresión se presenta en la ecuación que sigue:

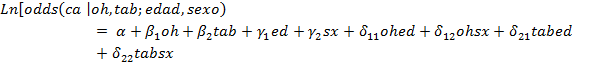
Esta notación permite identificar el rol de cada variable en el modelo de la siguiente forma: los 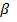representan los coeficientes de regresión correspondiente a los factores de exposición, los  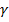representan los coeficientes asociados a las variables de control, y los  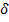representan a los coeficientes de los términos de interacción.

Una vez construido el modelo, el análisis de los datos se inicia probando la hipótesis que señala que no hay interacciones significativas, indicando que el efecto de los factores de exposición, consumo de alcohol  y consumo de tabaco, son independientes de la edad y sexo.  En lenguaje epidemiológico, lo que se desea probar es la hipótesis que establece que las variables de control no son modificadoras del efecto de la exposición en la variable de resultado. En el ejemplo, lo que se desea probar es si la edad y sexo de los pacientes son modificadores del efecto de consumo de alcohol y de consumo de tabaco sobre el cáncer de esófago.

Esta hipótesis está representada por la siguiente expresión:

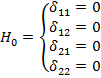
La decisión sobre rechazar o no esta hipótesis se basa en la llamada prueba de razón de verosimilitud que permite, en este caso particular, la evaluación simultánea de los cuatro coeficientes de regresión.

Un valor p por encima del nivel de significación predeterminado para esta prueba de hipótesis permite tomar la decisión de no rechazar H₀, con lo que se puede concluir que no existe evidencia suficiente para pensar que el efecto del consumo de alcohol y del consumo de tabaco sobre el cáncer de esófago dependa de la edad y sexo de los pacientes.

En este caso, se puede concluir que el modelo estadístico que responde a la pregunta de investigación es:

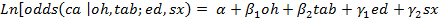
De esta forma, el efecto de alcohol y de consumo de tabaco, ajustado por edad y sexo, en cáncer de esófago es estimado respectivamente 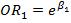por y por .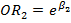 

El factor de exposición constituirá un factor de riesgo si el OR estimado es significativamente mayor que 1, y será factor de protección en caso de que sea significativamente menor que 1.

La respuesta a la pregunta de investigación es más compleja cuando la prueba de hipótesis sobre modificación de efecto tiene un valor p por debajo del nivel de significación predeterminado, indicado que al menos una de las variables de control modifica el efecto de al menos uno de los factores de exposición. Por simplicidad, se asume de ahora en adelante que la interacción consumo de alcohol con edad 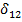 ( es el único coeficiente de regresión que resultó ser significativamente diferente de cero entre el conjunto de interacciones evaluadas. A partir de este resultado, lo que corresponde es hacer la estimación del efecto de consumo de alcohol en el cáncer de esófago en forma diferenciada según la edad de los pacientes.

El modelo que responde a la pregunta de investigación bajo esta condición es entonces:

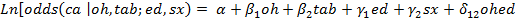
En este caso, la decisión sobre el efecto del consumo de alcohol se hace en forma diferenciada según la edad del paciente.

En pacientes menores de 60 años la estimación del efecto de consumo de alcohol, ajustado por consumo de tabaco y sexo  está dada por . En mayores de 60 años, la estimación corresponde a .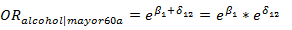

Asumiendo que el consumo de alcohol es factor de riesgo para cáncer de esófago, la diferencia de efecto está dada por el factor 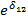, que de ser mayor que uno, indica que en los mayores de 60 años el efecto del consumo de alcohol sobre el cáncer de esófago es mayor que en los menores de 60 años. En caso que este factor sea menor que uno, indica que el efecto del consumo de alcohol es mayor en los menores de 60 años.

Conclusión

La herramienta que proporcionan los modelos de regresión es bastante poderosa, pero a la vez peligrosa si no se ocupa en forma debida. Es común encontrar en la literatura científica soluciones a preguntas de investigación de este tipo en que solo se considera a las variables de control como variables de ajuste en el estudio del efecto de factores de exposición en la ocurrencia de eventos de salud, y no se plantean la posibilidad de que dichos efectos no sean homogéneos entre pacientes que tienen diferentes características como son al menos las biodemográficas.

Notas

Declaración de conflictos de intereses
Los autores refieren no tener conflicto de intereses alguno con el tema del artículo.

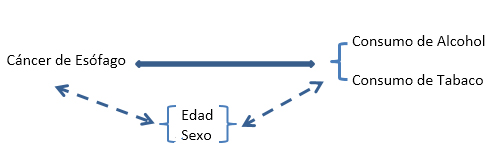Figura 1. Esquema de variables del estudio de asociación.

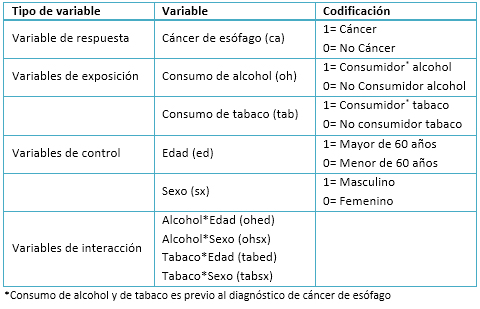Tabla 1. Especificación de las variables del Modelo.

Esta obra de Medwave está bajo una licencia Creative Commons Atribución-NoComercial 3.0 Unported. Esta licencia permite el uso, distribución y reproducción del artículo en cualquier medio, siempre y cuando se otorgue el crédito correspondiente al autor del artículo y al medio en que se publica, en este caso, Medwave.