1. Introducción

Al diseñar una investigación en salud pública o epidemiología, una de las preguntas que debe responderse el investigador es: “¿Cuántos sujetos necesito para mi estudio?”. Para poder responderla adecuadamente es necesario plantearse una serie de otras preguntas, entre las cuales están las siguientes: ¿Cuál es el objetivo del estudio? ¿El problema planteado corresponde a una estimación de una característica desconocida de una determinada población? ¿Cuál es la hipótesis principal del estudio? ¿Qué diseño de investigación ha sido el escogido para dar respuesta a la pregunta de investigación?

Adicionalmente, al problema de determinar el número de sujetos necesarios para el estudio, la pregunta que sigue es: “¿Cómo consigo que la muestra, cuyo tamaño sea este número de sujetos que se ha determinado, sea representativa de la población desde donde vamos a seleccionar estos sujetos?”

Este artículo intenta aportar a la determinación del número de sujetos necesarios para un estudio de tipo observacional, dejando para más adelante la discusión sobre opciones metodológicas que permiten de alguna manera, obtener una muestra representativa de sujetos de una o varias poblaciones.

2. Determinación de tamaño de muestra para estudios de corte transversal

El objetivo en un estudio de corte transversal es generalmente determinar la prevalencia de alguna condición de salud como, por ejemplo, prevalencia de consumo de alcohol en estudiantes de enseñanza media. Desde la perspectiva estadística, la metodología correspondiente es la de estimación de un parámetro, que en este caso es la prevalencia.

Con el fin de determinar el número de sujetos necesarios para hacer la estimación de dicha prevalencia, las interrogantes que siguen son: ¿Cuál es la prevalencia alrededor de la cual se espera encontrar en la población de origen? ¿Cuál es el margen de error aceptable para hacer esta estimación, o magnitud de la precisión deseada para la estimación de la prevalencia? Y finalmente, ¿con qué nivel de confianza se desea estimar la prevalencia?

Sólo para fines ilustrativos se presenta una fórmula de cálculo (la única de todo el artículo) para establecer el tamaño de muestra y obtener la estimación de prevalencia. Si n denota el tamaño de muestra a determinar, P representa la prevalencia esperada, y D corresponde al nivel de precisión absoluta deseada, definida como la distancia máxima a partir de la prevalencia esperada, y 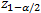es el valor de la distribución normal asociado a un nivel de confianza de 100(1-α) %, el tamaño de muestra se calcula mediante la siguiente fórmula: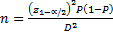

Supongamos que se desea estimar una prevalencia que se espera está alrededor de un 20%, y se consideraría que esta prevalencia estaría adecuadamente estimada incluso cuando se cometiera un error de hasta 2% en la estimación. Con un nivel de confianza de 95%, el tamaño de muestra es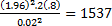

En muchas ocasiones se conoce el tamaño de la población (N) desde donde se desea estimar la prevalencia. En estos casos, el tamaño de muestra se debe ajustar por el llamado factor de corrección para poblaciones finitas definido como (fcpf=1/(1+n/N)).

En el ejemplo anterior, asuma que la prevalencia a estimar es en una población de 5000 sujetos. Con esto el fcpf=1+(1537/5000)=1,6926. De esta forma el tamaño de muestra corregido es de 1537/1,3074=1176 sujetos.

Más abajo se aprecia la determinación de tamaño de muestra para prevalencias usando el paquete estadístico Epidat. Epidat es un paquete estadístico de acceso libre, elaborado bajo el auspicio de la Organización Panamericana de la Salud, la Junta de Salud de Galicia y la Universidad CES de Colombia, y puede ser descargado desde https://www.sergas.es/MostrarContidos_N3_T01.aspx?

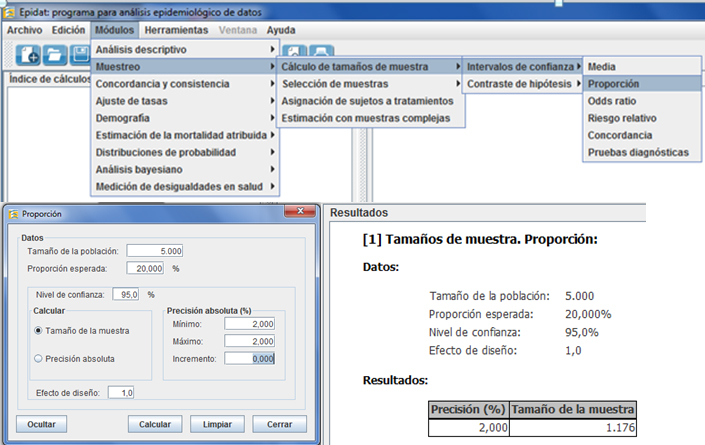
Una dificultad de orden práctico que presenta la formulación de supuestos para la determinación de tamaño de muestra en este tipo de estudios, tiene que ver con el hecho de que exige tomar decisiones subjetivas. Por ejemplo, al fijar la “prevalencia esperada”, es obvio que el usuario no puede conocer dicha magnitud, pues precisamente, el tamaño de muestra se ha de establecer para estimar esta prevalencia cuando contemos con la muestra propiamente tal. Esta circunstancia obliga incluso a especular sobre los datos que han de informarse al programa para que pueda proceder al cómputo del tamaño necesario. Siendo así, los resultados que se obtengan tendrán un carácter orientativo para el investigador, quien ha de proceder, sobre esas bases, a contemplar otros elementos complementarios asociados con el problema. Entre ellos se hallan el presupuesto disponible, el grado de conocimiento que ya se tenga sobre el problema que se aborda o los tamaños empleados en otros estudios similares.

3. Determinación de tamaño de muestra en estudios de cohortes

En un estudio de cohortes, el objetivo generalmente es determinar si un definido factor de exposición constituye o no un factor de riesgo o de protección para determinada condición de salud. A diferencia del caso de estudios de corte transversal, ahora el problema se resuelve mediante el planteamiento de una hipótesis estadística sobre el riesgo relativo, definido como la razón entre el riesgo de desarrollar el evento de salud de interés (en un periodo de tiempo determinado) en el grupo definido como expuesto y el riesgo en el grupo definido como no expuesto.

De esta forma, es necesario definir por parte de los investigadores lo siguiente:

1. Proporción de sujetos en el grupo no expuesto que se espera desarrollen el evento de salud en el periodo de tiempo predefinido (riesgo en no expuestos).
2. Alternativamente, se debe proporcionar una estimación de cuál sería la diferencia mínima de riesgo de desarrollar el evento en el grupo expuesto, de modo que el factor de exposición pueda ser considerado como factor de riesgo (o de protección); también puede planterase la hipótesis de cuál es el riesgo relativo a estimar, de modo que la exposición sea factor de riesgo o de protección.
3. Adicionalmente se debe especificar el nivel de significación y la potencia estadística (power).

Supongamos que se desea determinar el tamaño de muestra para un estudio de cohortes donde se plantea que el riesgo de enfermar en un año en el grupo NO expuesto es de un 8%. Se plantea que la exposición puede ser considerada como factor de riesgo, si el riesgo relativo es al menos de 2, con una significación de un 5% y una potencia estadística de 80%.

A continuación se presenta el cálculo de tamaño de muestra usando Epidat, usando una razón de 1 expuesto por cada no expuesto. Se necesita seguir por un año a 553 sujetos no expuestos y 553 sujetos expuestos a la condición de interés.

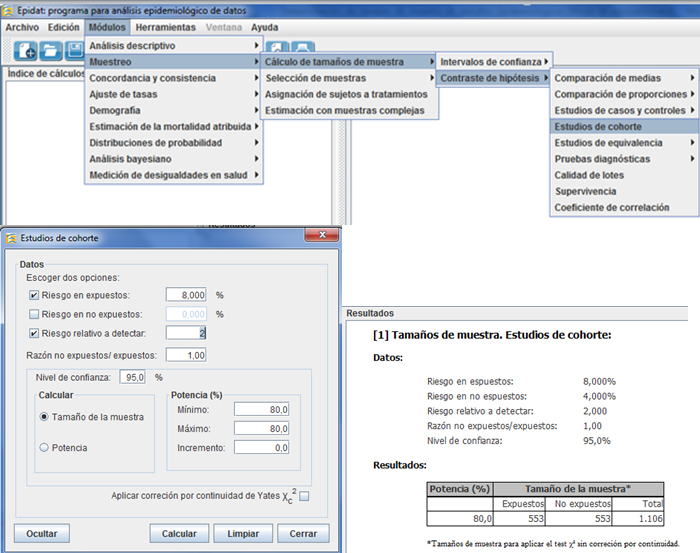
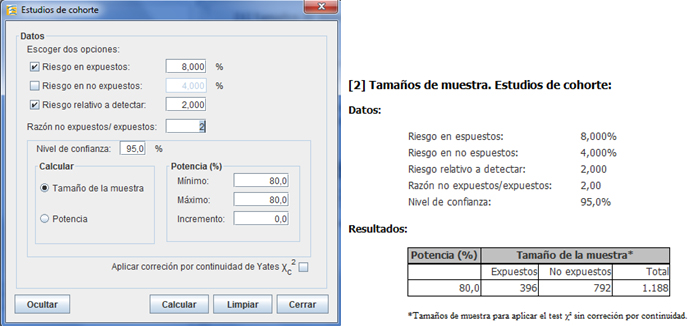
En ocasiones no es posible encontrar un número de sujetos expuestos como el determinado. En este caso, se puede recalcular el tamaño de muestra modificando la razón entre expuestos y no expuestos. En el ejemplo, el tamaño de muestra sería de 396 sujetos a seguir en el grupo de los expuestos y 792 en el de no expuestos. Nótese que el tamaño de muestra total es siempre menor cuando la razón de expuestos a no expuestos es de 1:1.

4. Determinación de tamaño de muestra en estudios de casos y controles

En estudios de casos y controles el foco se centra en la comparación de la prevalencia de exposición, en el grupo definido como casos con la de controles. Sin embargo, es más frecuente utilizar hipótesis sobre la odds de exposición en ambos grupos, debido a que se utiliza la razón de odds como medida de asociación a ser utilizada para evaluar, si la exposición de interés constutuye un factor de riesgo (o de protección) del evento de salud de interés para la investigación.

De esta forma, es necesario establecer de antemano los siguientes elementos para el cálculo de tamaño de muestra.

1. Prevalencia de exposición (proporción) en los controles (generalmente asumida como la de la población general).
2. Prevalencia esperada en los casos o razón de odds de exposición a modo de determinar que la exposición constituye factor de riesgo (o de protección) de la condición de salud bajo estudio.

Como ejemplo, considere la determinación de tamaño de muestra en un estudio donde la proporción de expuestos en población general es de 12% , y que se determina una razón de odds de 2 como mínimo, a modo de catalogar a la exposición como factor de riesgo de la enfermedad en estudio.

Usando Epidat, vemos que es necesario tomar una muestra de 245 casos y 245 controles.

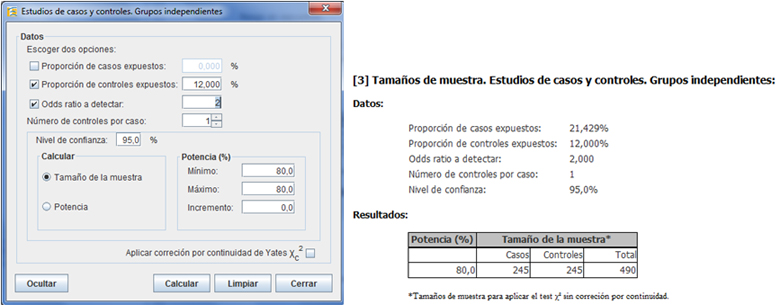
En caso de no poder contar con suficientes temas en el cálculo de tamaño de muestra, se puede modificar la razón de controles por caso como se muestra en el siguiente cálculo, donde se efectúa el cálculo de tamaño de muestra usando la razón de 2 controles por caso.

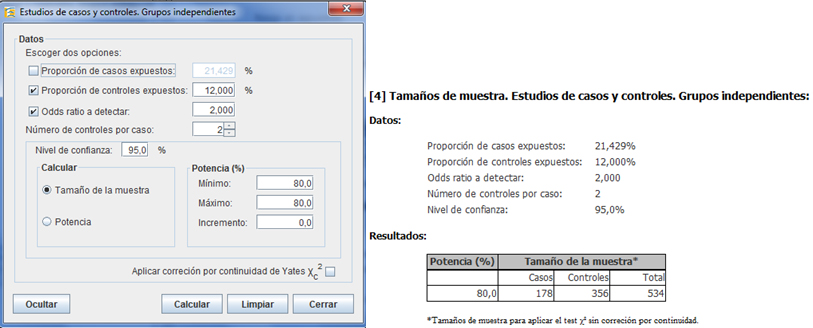
Se oberva que el tamaño de muestra total aumenta de 490 a 534 sujetos.

Tanto en estudios de casos y controles como de cohortes, es posible aumentar la razón de controles por caso o de no expuestos por expuestos, respectivamente, teniendo en cuenta que el tamaño mínimo de muestra siempre será usando la razon 1:1; razones de 4:1 o mayores no generan ganancias significativas en la reducción del número de casos en relación al número total de sujetos a incluir en el estudio.

5. Conclusiones y precauciones

Los procedimientos presentados en este trabajo tienen varios supuestos que deben ser validados antes de su uso. El principal es que se asume que el diseño muestral corresponde a muestreo aleatorio simple (MAS), lo que en la práctica no siempre es el caso. Muchas veces, ya sea por intentar conseguir representatividad o por la estructura compleja que puede presentar la generación de los datos, como puede ser muestreo por clínicas, por profesional de la salud u otro, el supuesto de MAS, que implica que las mediciones que se efectúan en los sujetos son independientes, no se satisface. Epidat proporciona la opciones para la determinación de tamaño de muestra para estudios, cuyo diseño muestral es complejo. Se sugiere revisar el menú de ayuda de dicho progama para detalles de uso de esta opción.

Es importante para el investigador tener absoluta claridad sobre los supuestos y antecedentes que debe aportar para el cálculo de tamaño de muestra, como los objetivos del estudio, existencia o no de hipótesis de trabajo, y diseño del estudio, entre otros.

Por lo demás, no se debe olvidar ajustar por eventuales rechazos a participar y por pérdidas de seguimiento cuando corresponda.

Notas

Declaración de conflictos de intereses
El autor ha completado el formulario de declaración de conflictos intereses del ICMJE traducido al castellano por Medwave, y declara no haber recibido financiamiento para la realización de la serie; no tener relaciones financieras con organizaciones que podrían tener intereses en el artículo publicado, en los últimos tres años; y no tener otras relaciones o actividades que podrían influir sobre el artículo publicado. El formulario puede ser solicitado contactando al autor.

Esta obra de Medwave está bajo una licencia Creative Commons Atribución-NoComercial 3.0 Unported. Esta licencia permite el uso, distribución y reproducción del artículo en cualquier medio, siempre y cuando se otorgue el crédito correspondiente al autor del artículo y al medio en que se publica, en este caso, Medwave.